1.构建小根堆
vector<int> arr;
void buildMinHeap(int firstIndex, int endIndex) {
for (int i = endIndex/2; i >= firstIndex; i--) {
adjustDown(i, endIndex);
}
}
void adjustDown(int parentIndex, int endIndex) {
int left = 2 * parentIndex + 1;
int right = 2 * parentIndex + 2;
//最小值的下标
int minIndex = parentIndex;
if (left < endIndex && arr[left] < arr[minIndex]) {
minIndex = left;
}
if (right < endIndex && arr[right] < arr[minIndex]) {
minIndex = right;
}
if (minIndex == parentIndex) {
return;
}
//交换元素
swap(parentIndex, minIndex);
//递归调整
adjustDown(minIndex, endIndex);
}
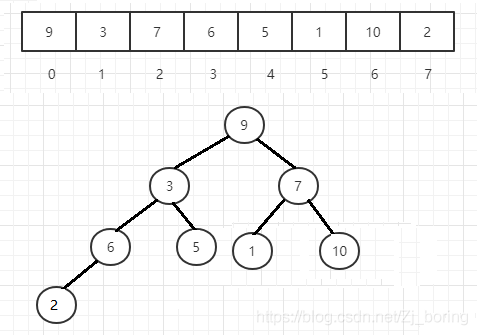
arr看做完全二叉树,直接下标关系
- _ leftNodeIndex = ParentNodeIndex*2 +1 _
- rightNodeIndex = ParentNodeIndex*2 +2
- _ParentNodeIndexl = childNodeIndex/2 _
从最后一个元素开始往上调整,即adjustDown(待调整子树根节点Index,末尾下标)
- 末尾下标:用于下表关系计算时判断是否越界
- 待调整子树根节点Index:如图,从6为根子树开始往前才是有子节点的
- 递归调整:从3为根的位置开始,交换swap,会导致子树不再是小根堆,立即向下递归纠正
2.Heap Sort
建立完小根堆后,最小元素再第一位(唯一性质),我们和末尾元素交换,并把末尾下标减一; 代表最后一个元素已经排序好了,然后重复调用adjustment(0, end-1);重复以上; 最终,得到的vector是一个从大到小的排序序列; 注:由于该调整策略 ,堆排序不稳定(易举例)
void heapSort() {
int n = arr.size();
//1. 将数组构建成小根堆
buildMinHeap(0, n);
//2. 将堆顶元素(最小值)与堆底元素交换,并将堆的大小减1
for (int i = n - 1; i > 0; i--) {
swap(0, i);
//3. 对剩下的元素重新进行堆化
adjustDown(0, i);
}
}
3.LeetCode相关练手题
C++ 【时间:击败95%】【空间:击败100%】【特色:原地空间O(1)解法】 https://leetcode.cn/problems/total-cost-to-hire-k-workers/solutions/2348255/tiao-zhan-o1kong-jian-fu-za-du-shuang-du-u2m3/?envType=study-plan-v2&envId=leetcode-75